Section 2: Gravity Surveying

Introduction

Gravity surveys measure the acceleration due to gravity, g. Average value of g at Earth’s surface is 9.80 ms^-2.

Gravitational attraction depends on density of underlying rocks, so value of g varies across surface of Earth.

Density, r, is physical parameter to which gravity surveys are sensitive.

Examples

• Micro-gravity: location of subsurface cavities, location of tombs (low density of air relative to soil/rock)

• Small scale: mapping bedrock topography (high density bedrock relative to soil), mineral exploration (high density massive ore body relative to host rock)

• Medium scale: location of salt domes in oil exploration (low density salt relative to sediments)

• Large scale: estimation of crustal thickness (low density crust over higher density mantle)

Newton’s Law of Gravitation

Gravity surveying is based on Isaac Newton’s Universal Law of Gravitation, described in Principia Mathematica in 1687.

Newton’s Universal Law of Gravitation

The force of attraction between two bodies of known mass is directly proportional to the product of the two masses and inversely proportional to the square of the distance between them.

where M and m are the masses of the two bodies, r the distance separating them, and G=6.67 x 10^-11 Nm²kg^-2 is the gravitational constant.

On the Earth:

For a mass on the surface of a uniform spherical Earth of mass M and radius R, the gravitational attraction on a small mass m is given by:

g m is the weight of the mass, and g is the acceleration due to gravity, or just gravity. g = 9.80 ms^-2 on average.

Units of Gravity

Galileo made the first measurement of the acceleration due to gravity by dropping objects from the leaning tower of Pisa.

• In honour of Galileo, the c.g.s. unit of gravity is called the Gal.

1 Gal = 1 cm s^-2

Modern gravity meters are extremely sensitive and can measure g to within 1 part in 10⁹. (Equivalent to measuring the distance from the Earth to the Moon to within 1 metre).

• So the c.g.s unit commonly used in gravity measurement is the milliGal:

1 mGal = 10^-3 Gal = 10^-3 cm s^-2

• In m.k.s. SI units, gravity is commonly measured in mm s^-2 or g.u. (gravity unit).

10 g.u. = 1 mGal

Both mGal and g.u. are commonly utilised in gravity surveying.

Example

What is the value of g in mGal?

g = 9.80 ms^-2 = 9.8 x 10⁶ mm s^-2 = 9,800,000 g.u.

= 980,000 mGal

Accuracy of Gravity Measurement

On land: ± 0.1 g.u.

At sea: ± 10 g.u. (due to motion of ship)

Shape of the Earth

If the Earth were a uniform sphere g would be constant. However, gravity varies because the density varies within the Earth and the Earth is not a perfect sphere.

• The Earth has the shape of a flattened sphere because of its rotation.

• The radius is greater at the equator because the greater centrifugal force tends to pull material outward.

R_Equator = R_Pole + 21 km = 6378 km

· The Earth’s shape is described mathematically as an ellipse of rotation, or an oblate spheroid.

• The topography of the Earth’s surface is also an important effect on the measured gravity.

The Geoid

The sea-level surface, if unaffected by tides or winds, is called the geoid.

• On land, the geoid is the surface that would correspond to the water level in imaginary canals cut through the continents.

• The geoid represents a surface on which the gravitational field has the same value, and so is called an equipotential surface. [If the gravity value varied, there would be a gravitational force that would force water to flow from one place to another.]

• The force of gravitational attraction is a vector, and is everywhere perpendicular to the geoid.

• The direction of gravity deviates from the vertical due to long wavelength features such as the continents and to short wavelength features such as a sulphide ore body.

• Thus the geoid deviates from the ellipse of rotation.

Geoid vs. Ellipse of Rotation

The difference between the average geoid at a latitude around the earth shows the effect of the long wavelength variations.

There are also extremes in the geoid over India, -80 m, and the western Pacific, +60 m, relative to ellipse of rotation.

Variation of Gravity with Latitude

Gravity is 51860 g.u. greater at the poles than at the equator. The acceleration due to gravity varies with latitude due to two effects:

1. Earth’s shape: radius is 21 km greater at equator so g is less

2. Earth’s rotation: Centrifugal acceleration reduces g. Effect is largest at equator where rotational velocity is greatest, 1674 km/h. Zero effect at poles.

For a uniform ellipse of rotation, the measured gravity is the resultant of the gravitational attraction vector and the centrifugal acceleration vector.

International Gravity Formula

The angle f defines the geographic latitude.

In 1743, Clairaut deduced a formula that expressed the variation of gravity with latitude.

This has been incorporated into the International Gravity Formula:

where g₀ is the gravity at sea level at the equator and f the latitude.

The most recent standard derived from the IGF is the 1967 Geodetic Reference System (GRS67), given by:

where

g₀ = 9.78031846 m s^-2

a = 0.005278895

b = 0.000023462

Note that there is an older 1930 standard, and surveys that use this will exhibit differences from the 1967 standard unless corrected (see Reynolds Box 2.4).

Densities of Geological Materials

We must know the density of typical subsurface rocks accurately to interpret gravity data. The table below gives common ranges and average values for density in Mg m^-3.

Densities of Sedimentary Rocks

Sedimentary rocks exhibit the greatest range of density variation due to factors such as:

• Mineral composition
• Cementation
• Porosity
• Pore fluid type

Typically the contrast between adjacent sedimentary layers is less than 0.25 Mg m^-3.

Density is increased by depth of burial:

• Sandstones and Limestones: density is increased by infilling of the pore space, not by volume change.

• Shales: density increased by compaction, and ultimately recrystallisation into minerals with higher densities.

Densities of Igneous Rocks

Igneous rocks tend to be denser than sedimentary rocks, with the density controlled primarily by silica content:

• Mafic rocks are thus more dense than felsic.
• Ultramafic rocks are most dense

The range of density variation tends to be less than in sediments as porosities are typically lower.

Measurement of Gravity

There are basically two type of gravity measurement:

Absolute Gravity

Measured under laboratory conditions using careful experiments employing two possible methods:

• Falling body

• Swinging Pendulum

Used to provide absolute values of g at network of worldwide sites such as National Physical Laboratory in UK or National Bureau of Standards in USA. (International Gravity Standardisation Net 1971, IGSN 71).

Relative Gravity

In most applications, only the variation of gravity relative to a base station (which can often be related to IGSN 71) is necessary.

Gravity readings are recorded at secondary stations such that the difference relative to the base station is well known.

The spacing of gravity stations varies:

• 2-3 per km² for regional surveys
• 8-10 per km² for hydrocarbon exploration
• 5-50 m grid for high resolution work, e.g. archeology
• 0.5 m for microgravity work

Accuracy

On land, achieving an accuracy of ±0.1 mGal (or 1g.u.) requires that:

• latitudinal position be known to ±10 m
• elevation above mean sea level, i.e. geoid, be known to ±1 cm

Many different instruments for measuring ralative gravity

Pendulum-Based Gravity Meters

Gravity first measured using a pendulum by Pierre Bouguer in 1749. Method commonly used up to 1930s in hydrocarbon exploration.

Period of a Pendulum

Gravity is inversely proportional to the square of the period of oscilation, T, of a swinging pendulum:

where L is length of pendulum.

If pendulum swung under identical conditions at two locations, relative change in g can be found:

Spring-Based Gravimeters

Gravimeters, essentially a mass suspended from a sophisicated spring balance, have been used to measure relative gravity since 1930s.

As weight of mass (mass x gravity) increases, the spring is stretched.

Hooke’s Law

Amount of extension of spring, dl, is proportional to extending force.

In gravimetry, extending force is change in gravity, dg, and spring constant, k, is known:

Variations in g are small, so need to meaure very small values of extension. For 30 cm long spring, change in length is ~3x10^-8m (30 nm, which is less than wavelength of light at ~500 nm).

Mechanism for amplifying spring extension required so it can be measured.

Stable Gravimeters

Stable gravimeters consist of a mass at end of a beam, which pivots on a fulcrum, and is balanced by a tensioned spring.

Changes in gravity affect weight of mass, which is balanced by restoring force of spring.

Askania Gravimeter

Beam is pivoted on main spring. A beam of light is reflected from the mass to a photoelectric cell. Deflection of mass, displaces light beam and changes voltage in circuit.

Retensioning auxiliary spring restores beam to null position, i.e. same position at which all measurements made.

Stable Gravimeters Using Electrical Amplification

Some gravimeters, including the common Scintrex CG-3, use the small extension of the mass to change the capcitance in an electric circuit.

Boliden Gravimeter

Mass is in form of a bobbin with two metal plates suspended between two other metal plates.

• Change in gravity causes mass to move and changes capacitance between top plates -- detected by tuned circuit.

• Mass returned to null position by adjusting DC current connected two lower plates—mass supported by electrostatic repulsion.

Scinntrex CG-3 Gravimeter

CG-3 operates on same principle, but uses feedback circuit to control current to plates that restores mass to null position.

Unstable (Astatic) Gravimeters

In a stable system, mass will return to equilibrium position after small disturbance. In unstable system, mass continues to move.

Example

• Stable: pencil lying flat on table. Lift up one end; it falls back flat

• Unstable: Pencil standing on end. Push it; it falls over.

Unstable gravimeters use mechanical instability to exaggerate small movement due to change in gravity.

• Horizontal hinged beam supports mass at end. Turning moment due to mass is mglcosq.

• Beam supported by spring connected above hinge. Turning moment due to spring proportional to perpendicular distance d.

• Increase in gravity extends spring, but shortens d reducing increase in restoring force and allowing greater movement (need to adjust geometry precisely).

LaCoste-Romberg Unstable Gravimeter

• Spring is metal with high thermal conductivity to minimise effects of thermal expansion/contraction. Thermally insulated.

• Spring is zero-length, i.e. pretensioned during manufacture so behaves as if it would contract to zero length if tension lost.

• Zero length spring is weak, and maximises extension.

• Mass is large.

• Reading made by viewing light reflected from beam in eyepiece.

• Null position recovered by adjusting micrometer screw.

• Long length of screw means meter can read over range of 50,000 g.u.; used for worldwide surveys. Accurate to 0.03 g.u.

Worden Unstable Gravimeter

• For thermal problem, made of quartz glass springs, rods, and fibres. (Quartz less sensitive to heat than metal).

• Assembly housed inside vacuum flask with electrical thermostat.

• Range of instrument is 20,000 g.u. with accuracy up to 0.1 g.u., but 1 g.u. more usual.

• Lower range means it is more commonly used for local surveys, over which g changes less.

Shipborne Gravimeters

Static Measurement

• Use remote-controlled land instrument in waterproof housing, which is lowered to seafloor.

• Accuracy almost as good as land, but often impractical.

Continuous Measurement

• Gravimeter mounted on gyro-stabilised horizontal platform, so meter responds to vertical motions only.

• Horizontal motion due to yawing of ship eliminated.

• External accelerations due to waves attenuated by heavy damping of suspension, and averaging reading over longer period than wave motion (>8 s).

• External motions can cause variations in measured gravity up to 10⁶ g.u.. With use of platform and corrections, accuracy is ±10 g.u..

• Variation of LaCoste-Romberg often used.

Corrections to Gravity Observations

Instrument Calibration Factor

Reading on gravimeter must usually be multiplied by calibration factor to get value of observed gravity, g_obs.

Reduction to Geoid

Before interpretation, raw gravity data must be corrected to common measurement datum such as mean sea level (geoid).

Gravity Anomaly

Difference between the observed anomaly and the value of the International Gravity Formula, e.g. GRS67, at the same location is the Gravity Anomaly with which we work.

Summary of Gravity Data Corrections

Several corrections must be applied to observed gravity to obtain sea level reference and anomaly:

Instrumental Drift

Drift

Gravimeters are very sensitive instruments. Temperature changes and elastic creep in springs cause reading to change gradually with time.

Drift is monitored by repeating reading at same station at different times of day, perhaps every 1-2 hours, to produce a drift curve.

Instrument drift correction for each station can be estimated from drift curve.

Example

Drift curve for survey shown above. For reading taken at 12:30 hrs, observed gravity reading should be reduced by d.

Drift values are typically < 10 gu per hour. Larger values indicate an instrument problem.

Earth Tides

Solid Earth responds to pull of Sun and Moon just like oceans, but movement is much less.

Pull of Sun and Moon large enough to affect gravity reading. Changes g_obs with period of 12 hours or so.

Earth tide corrections can be corrected by repeated readings at same station in same way as instrument drift.

Correction can also be made using published tables, e.g. Tidal Gravity Corerctions for 1991.

Latitude Correction

Gravity anomaly values obtained by subtracting theoretical value of gravity defined by International Gravity Formula, g_f

Local Latitude Correction

Approximate correction can be applied to small-scale surveys (<100 km), not tied in to absolute gravity network through base station readings.

• Horizontal gravity gradient determined at local base station from latitude:

gu per km

• Gravity increases towards poles, so latitude correction is more negative towards poles (as subtracted), i.e. with northward distance in northern hemisphere or southward distance in the southern hemisphere.

• At 51^o N, local latitude correction is around 8 gu/km.

• Latitude must be known ±10 m for surveys with accuracy of ±0.1gu.

Free-air Correction

Corrects for reduction in gravity with height above geoid, irrespective of nature of rock below.

Free-air correction is difference between gravity measured at sea level and at an elevation, h, with no rock in between.

Free-air Correction = 3.086 g.u./m = 3.086 h g.u.

• Correction is positive above sea level (i.e. added), negative below.

• Varies slightly with latitude from 3.083 g.u./m at equator to 3.088 g.u./m at poles.

• With usual gravimeter measurement accuracy of 0.1 g.u., elevation must be known to within 5 cm!!!

Free Air Anomaly

Free-air Anomaly is obtained after application of latitude and free-air corrections.

• FA anomaly maps commonly used for ocean areas.

Bouguer Correction

Free-air correction takes no account of rock mass between measurement station and sea level.

Bouguer correction, dg_B, accounts for effect of rock mass by calculating extra gravitational pull exerted by rock slab of thickness h and mean density r.

• Assumes flat topography. In rough areas terrain corrections required.

On land:

g.u.

where r is in Mg m^-3 and h is in metres.

At sea:

where h is the water depth.

Bouguer Anomaly

BA is Free-air Anomaly after subtraction of Bouguer correction.

Nettleton’s method

Bouguer correction quite sensitive to value of density used.

Example

With 250 m elevation, an 0.1 Mg m^-3 error in density will produce an error of 10gu.

The Bouguer Anomaly should show no correlation with topography, but an incorrect choice of density will reflect the topography.

Nettleton developed method of calculating BA using various trial density values. Correct density corresponds to BA correction that shows no correlation with topography.

Elevation is 76 m (250 ft). Correct density is 2.3 Mg m^-3

Terrain Corrections

Bouguer correction assumes subdued topography. Additional terrain corrections must be applied where measurements near to mountains or valleys.

If station next to mountain, there is an upward force on gravimeter from mountain that reduces reading.

If station is next to valley, there is an absence of the downward force on gravimeter assumed in Bouguer correction, which reduces free-air anomaly too much.

In both cases, terrain correction is added to Bouguer Anomaly.

Example of terrain correction

a. Gravity station at elevation h above geoid

b. Infinite rock mass assumed for Bouguer correction

c. Terrain correction compensates for error A in BC and also B

Hammer Charts

Terrain corrections can be computed using transparent template, called a Hammer Chart, which is placed over a topgraphic map.

• Chart is centred on gravity station and topography read off at centre of each segment.

• Contribution to terrain correction is obtained from tabulated values for each segement and then summed to obtain total correction. (See Table 2.8 in Reynolds).

• Based on formula for gravitational attraction of cylindrical segment.

• Considered an additional part of Bouguer correction, i.e. results in Bouguer Anomaly.

Eötvös Correction

If gravimeter is in moving vehicle such as ship or plane, it is affected by vertical component of Coriolis acceleration, which depends on speed and travel direction of vehicle.

gu

where f is geographic latitude and V is vehicle speed in knots.

Two components:

• Outward acting centrifugal acceleration due to movement of vehicle over curved surface of Earth.

• Change in centrifugal acceleration due to movement relative to Earth’s rotational axis. If vehicle moves east, it’s rotational speed is increased; if west, its speed is reduced.

Isostatic Correction

If no lateral density variations in Earth’s crust, Bouguer Anomaly would be the same, i.e. Earth’s gravity at the equator at geoid.

Bouguer anomaly positive over oceans, negative over mountains.

If crust is floating on mantle like an iceberg in ocean, total mass summed over any vertical column is the same. (Isostasy)

Airy Isostasy

Airy proposed that crust is thicker beneath mountains and thinner beneath the oceans.

Excess mass under the oceans from a shallower, high density mantle. Mass deficiency beneath mountains due to crustal root.

Pratt Isostasy

Pratt proposed that observation could be explained by lateral changes in density within a uniform thickness crust.

Airy Isostatic corrections can be applied to remove these long wavelength variations, isolating upper crustal anomalies.

Regional and Residual Anomalies

Bouguer Anomaly maps contain:

• Regional anomaly: long wavelength features due to deep crustal features
• Residual anomaly: short wavelength anomalies due to shallow structures

Residual must be separated for interpretation. Smoothed trend is fitted to BA graphically or by computer.

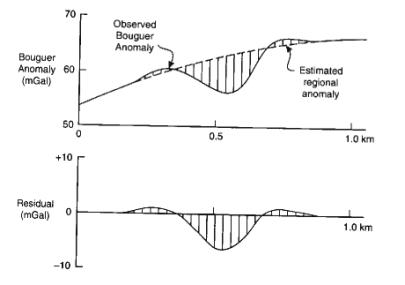
Example of Bouguer Anomaly and regional field:

Interpretation of Gravity Anomalies is Non-Unique

As with interpretation of many geophysical data, interpretation of gravity is ambiguous.

Example

Residual anomaly from a 600m radius sphere of 1.0 Mg m^-3 at 3 km depth also be produced by each of the bodies shown.

Interpretation can proceed by forward modelling or inversion methods.

Calculating Gravity Anomalies of Simple Bodies

Gravity anomaly of a body can be calculated by summing contribution of its component elements using computer.

For simple bodies, anomaly can be calculated simply:

Sphere or Point Mass

For point mass at distance r, gravitational attraction given by:

Gravimeter only measures vertical component, so anomaly is projection onto vertical:

Since attraction due to sphere is same as that of same mass at centre, this is formula for anomaly of buried sphere. (3-D case)

Horizontal Cylinder

Can integrate above formula to get result for horizontal cylinder(2-D case):

where m is mass per unit length.

Gravity Anomalies of Spheres and Cylinders

Anomaly shape can be plotted using formula. Anomaly from sphere decays more quickly than that of horizontal cylinder.

Vertical cylinder has different shape with steeper flanks:

Depth Estimation by Half-Width Method

Using the formulae for the anomalies due to various bodies, it is posible to estimate the limiting depth of a body.

Limiting depth is maximum depth at which top of body could occur to produce anomaly. (Body could be shallower).

Half-Width Method

Half-width, X_1/2 , is the distance from the centre of an anomaly at which amplitude has decreased to half its peak value.

If anomaly is spherical:

If anomaly is horizontal cylinder:

If anomaly is vertical cylinder:

If anomaly is thin steeply dipping sheet:

Depths are overestimates as based on centre of mass of body.

Depth Estimation by Gradient-Amplitude Method

Can obtain estimates of limiting depth from maximum slope also.

If value of maximum slope, Dg’_max , estimated:

For 3-D body:

For 2-D body:

Mass Estimation

Anomalous Mass is difference between mass of anomalous body and mass of body replaced with host rock.

• Anomalous mass can be uniquely determined from gravity anomaly, but important that regional be correctly removed.

• Anomaly divided into series of rings, each of which is divided into further segments, dA_i.

If Dg_i is value of residual anomaly in segment,

Total Anomalous Mass given by:

Actual mass can be determined simply from anomalous mass if densities of anomaly and host rock are known:

where r₁ is density of body, and r₀ density of host rock.

• If body less dense than surrounding rock, anomalous mass will be negative, mass deficiency.

• Important method for estimating ore reserves.

Application to Salt Domes

Average density of salt, 2.2 Mg m^-3, is less than most sediments in a basin, so salt often rises in diapir due to its bouyancy.

Makes good target for gravity surveys, and will show up as a bullseye anomaly.

Example: Mors salt dome, Denmark

Studied for radioactive waste disposal. Dots are gravity stations.

From profile across anomaly:

• Maximum amplitude of residual anomaly = 16 mGal
• Anomaly half-width= 3.7 km

Assuming salt dome represented by sphere, limiting depth, i.e. depth to centre of mass = 4.8 km

Assuming density contrast of –0.25 Mg m^-3, radius of sphere estimated at 3.8 km. So top of salt at 1 km depth.

Best model obtained by forward modelling of gravity data:

Compare inferences from gravity with best model derived from all methods, including seismic reflection and drilling.

Application to Massive Sulphide Exploration

Massive sulphide ore bodies have high densities due to minerals present.

Can show as gravity high in residual anomaly.

Example: Faro Pb-Zn deposit, Yukon

Gravity proved to be best geophysical technique to delimit deposit

Tonnage of 44.7 million estimated from gravity, which compares with drilling estimate of 46.7 million.

Application to Detection of Underground Cavities

Buried cavities due to old mine workings can be a significant hazard!

Result of catastrophic failure of roof of ancient flint mine in chalk.

Cavities can be good target for micro-gravity due to high density contrast between a void, or rubble-filled void, and host rock.

In practice, many anomalies are greater than predicted by theory.

Example: Inowroclaw, Poland

Karst caverns in subsurface composed of gypsum, anhydrite, dolomite, and limestone. Develop towards surface and destroy buldings.

Density contrasts are around -1.8 Mg m^-3 and -1.0 Mg m^-3 for void and rubble-filled void.

Rubble-filled void should not have been detectable from calculated anomaly.